Albers equal-area conic

Parameters: Latitude of origin, Standard parallel 1, Standard parallel 2

Classifications

conic
equal-area

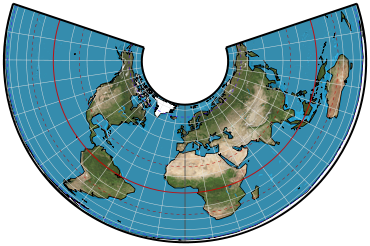
Graticule

Meridians: Equally spaced straight lines converging at a common point, which is normally beyond the pole. The angles between them are less than the true angles.
Parallels: Unequally spaced concentric circular arcs centered on the point of convergence of the meridians. The meridians are therefore radii of the circular arcs. Spacing of parallels decreases away from the central latitudes.
Poles: Normally circular arcs enclosing the same angle as that enclosed by the other parallels of latitude for a given range of longitude.
Symmetry: About any meridian.

Aspects

Rarely used in oblique aspect but occasionally proposed in journal articles.

Limiting forms

Polar Lambert azimuthal equal-area projection, if a pole is made the single standard parallel. The cone of projection thereby becomes a plane. Lambert equal-area conic projection, if the pole and another parallel are made the two standard parallels Lambert cylindric equal-area projection, if the equator is the single standard parallel. The cone of projection thereby becomes a cylinder. Behrmann or other cylindric equal-area projections, if the two standard parallels are symmetrically placed north and south of the equator. Standard conic formulas must be rewritten for the third and fourth limiting forms.

Scale

True along one or two chosen standard parallels, usually but not necessarily on the same side of the equator. As a rule of thumb, these parallels can be placed at one-sixth and five-sixths of the range of latitudes, but there are more refined means of selection. Scale is constant along any given parallel. The scale factor at any given point along the meridian is the reciprocal of that along the parallel, to preserve area.

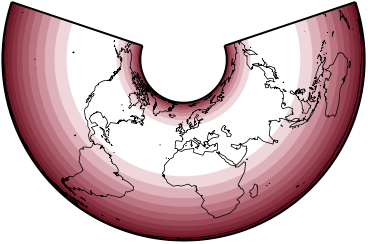
Distortion

Free of angular and scale distortion only along the one or two standard parallels. Distortion is constant along any given parallel.

Usage

Frequently used in the ellipsoidal form for maps of the United States in the National Atlas of the United States, for thematic maps, and for world atlases.
Also used and recommended for equal-area maps of regions that are predominantly east-west in extent.

Similar projections

Various methods of determining optimum standard parallels have been proposed by N.A. Tissot in 1881, V.V. Vitkovskiy (projection 11) in 1907, N.Ya. Tsinger in 1916, and F.N. Krasovskiy (projection l) in 1922. Once the standard parallels are selected, all these projections are constructed by using the same formulas used for the Albers equal-area conic with two standard parallels.

Origin

Presented by Heinrich Christian Albers (1773 – 1833) of Germany in 1805.

Description adapted from J.P. Snyder and P.M. Voxland, An Album of Map Projections, U.S. Geological Survey Professional Paper 1453. United States Government Printing Office: 1989.