daan wrote:I have my ideas, but nobody knows. I can give you a hint about what the optimal equal-area map of the whole world, split along one meridian, might look like, though. The next map is on what I call the “Dietrich–Kitada” projection. Bruno Dietrich was the author of a 1927 German text,
Grundzüge der allgemeinen Wirtschaftsgeographie. The curious thing about this text is that it is illustrated with many full-page thematic maps, all in a single map projection, one whose construction method is… unknown, as far as I know. In late 1957, in a paper titled
世界全図に適する新図法の提出まで(続) (“Presenting new map projections for whole-world maps (continued)”), a Japanese mathematical cartographer named Kōzō Kitada (北田 宏蔵) described the projection he found in this German text, ascertained that it was equal-area, or at least nearly so, and set about formulating a recreation of it. He set the meridians to circular arcs, bounded the front hemisphere by a full circle, and determined the parallel shapes required to preserve area with these constraints. This is what he came up with:
Dietrich-Kitada.jpg
The true optimal map will look somewhat different than this, but this is the gist.
This statement of yours just may have proven prophetic.
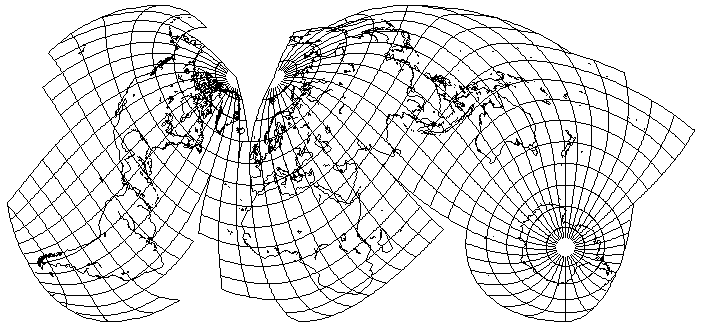
After learning about the Dietrich-Kitada projection from this post, I implemented it in my crude BASIC-language map-drawing program, and played around with drawing it in a few different aspects. I only managed to find one, centered near Moscow, that made a tolerable world map; the Dietrich-Kitada has a large area of low error, but also a large area of high error, and its distribution of error seems perverse.
One of the maps I drew was in a transverse aspect - specifically because there were some similarities to the Dietrich-Kitada and the Mollweide (or should that be the
transverse Mollweide). The shape of the meridians suggested to me that an interesting projection might be obtained by subjecting the Dietrich-Kitada projection to the same process used by Gott with the Mollweide.
Here is the projection that resulted:
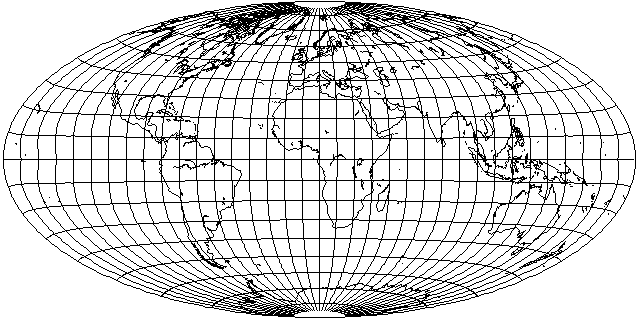
The world is placed on a 2:1 ellipse, as with the Mollweide and the Hammer. But the central portion of the projection... looks almost like an equal-area cylindrical. In conventional aspect, it's not all that great, but as it has a large low-distortion area around the Equator, it may be easier to find a useful aspect for this projection than it was for the original Dietrich-Kitada.
And indeed it was:
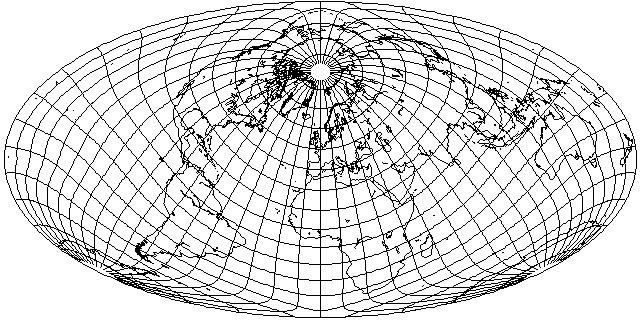
Using the same aspect as Bartholomew's Nordic... I get a surprisingly good-looking Australia and New Zealand, thanks to its cylindrical-like nature near the Equator.
Oh, and as the scale is uniform along the Equator, this projection can even be
interrupted. That could provide interesting possibilities - and, of course, it could be squashed, like the Bromley-Mollweide, to get rid of the Equatorial stretch if desired.
Having tried a few other orientations with this projection, though, even though it clearly differs from the Mollweide, it doesn't seem that the differences are great enough to yield any benefits that would justify all the extra calculation.
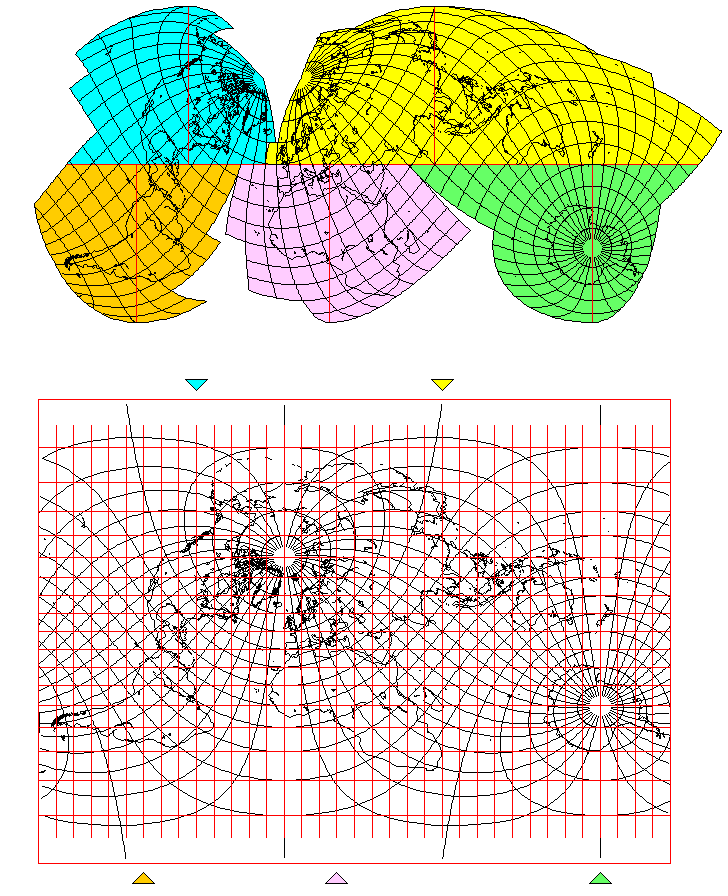
All this inspired me to do something involving less fancy calculation; to go back to the Mollweide, and come up with this interrupted oblique Mollweide which keeps Eurasia in one piece - and Antarctica - and, as much as possible, the South Pacific islands as well!
In the event this projection generates any interest, I added an explanatory image describing it.