Which projections you favor?

[quadibloc]

I certainly agree with Daniel Strebe that different projections serve different purposes, and so you can't just use one favorite projection for everything.
But that doesnt mean one can't have a "favorite projection" or two - I've seen a few projections I liked, often because they were particularly low in shape distortion.
I think my all-time favorite is Bartholomew's Regional Projection, specifically the modified version that was conical to the poles that appeared in the Times World Atlas.
That's despite the fact that there is a kink in the projection where the conical part joins the Bonne's part (actually, in the Times version, but not the earlier ones, they fudged the projection slightly to get rid of the kink) which is an attribute that turned me against Goode's Homolosine projection.
As for my own projections, I've played with an interrupted Bonne's, and with putting the world on two hemispheres (the conventional Eastern and Western ones, divided at 20 degrees West) each displayed on a (transverse) conic conformal.
Also, I prefer the Hammer-Aitoff to the Mollweide, and the Miller Cylindrical to the Gall Stereographic; I'd rather not have too much equatorial stretching in a projection.
I am enraptured also by the beauty of some exotic projections, even though I admit they're not practical for every-use; the conformal projection on an octahedron using Dixon elliptic functions, and Guyou's Doubly-Periodic projection using ordinary elliptic integrals, and August's conformal.
And the Van der Grinten IV is a nice compromise projection that's easy to draw. Not only that, but the scale is uniform all the way across the Equator. So, although nobody else, to my knowledge, has ever tried it, you can interrupt it just the same way you can interrupt a Sinusoidal or a Mollweide.

[RogerOwens]

I certainly agree with Daniel Strebe that different projections serve different purposes, and so you can't just use one favorite projection for everything.

Yes, for world maps, I use the Mercator wall-map, and the various equal-area maps that my atlases have.

(We also have a Gall Stereographic wall-map on the wall, in the most prominent display-space in our apartment, because we like its style, quite aside from its projection (and because Mercator now can't be found in stores). And of course most often, when one refers to a world-map, equal-area and conformality aren’t really necessary (though, given a choice, I prefer for a world-map to have one of those properties) ).

My favorite world-maps now are Mercator, Mollweide, Behrmann, and my Optimal CEA-Stack.

I feel that Mercator, Mollweide and Behrmann are under-rated.

Also, I prefer the Hammer-Aitoff to the Mollweide

Yes, Hammer-Aitoff has better shapes, at the cost of non-pseudocylindricalness. Pseudocylindrical and Cylindrical maps (I call a map “Cylindroid” if it’s Cylindrical or Pseudocylindrical) have many practical advantages. Yes, Mollweide’s Africa is a bit skinny, but its straight parallels are more globe-realistic, because a globe’s parallels appear straight in a distant equatorial view.

, and the Miller Cylindrical to the Gall Stereographic; I'd rather not have too much equatorial stretching in a projection.

Yes, Gall Stereographic distorts tropical shapes, particularly noticeable with Africa, and I, too, would prefer otherwise.

But tropical shape-distortion is the price for Gall Stereographic’s conformality at lat 45 (+ & -). Gall probably wanted a worldwide shape-compromise. Conformality at lat 45 could be called Eurocentric, but it can also be regarded as a worldwide shape-compromise.

Likewise with Behrmann vs Lambert:

Behrmann’s tropical shapes are acceptable, aesthetically perfectly alright, while its NS scale at lat 60 is still 2/3 of its equatorial-scale, and its NS scale at North-Cape is still 43% of its equatorial-scale.

Its flattening of arctic shapes isn't so unrealistic, because that region is NS foreshortened in an equatorial view of a globe.

Michael Ossipoff
August 18th
34 Su
2035 UTC

[daan]

Yes, Gall Stereographic distorts tropical shapes, particularly noticeable with Africa, and I, too, would prefer otherwise.
…
Behrmann’s tropical shapes are acceptable, aesthetically perfectly alright, while its NS scale at lat 60 is still 2/3 of its equatorial-scale, and its NS scale at North-Cape is still 43% of its equatorial-scale.

I have to suppose you mean Gall orthographic (which is equal-area), not Gall stereographic (which is not equal-area). Gall stereographic elongates Africa less than Behrmann.

— daan

[RogerOwens]

I have to suppose you mean Gall orthographic (which is equal-area), not Gall stereographic (which is not equal-area).

No, I meant Gall Stereographic. I was replying on the matter of Gall Stereographic vs Miller-Cylindrical. Then I mentioned Behrmann vs Lambert as another example of all-world compromise vs equatorial conformality.

Gall stereographic elongates Africa less than Behrmann.

Sure, but both are acceptable to me. And of course Behrmann give you something (equal-area) in return, which, for me, fully justifies its minor (4:3) equatorial proportions distortion.

Michael Ossipoff
August 18th
34 Su
2115 UTC

[quadibloc]

I've played with an interrupted Bonne's, and with putting the world on two hemispheres (the conventional Eastern and Western ones, divided at 20 degrees West) each displayed on a (transverse) conic conformal.

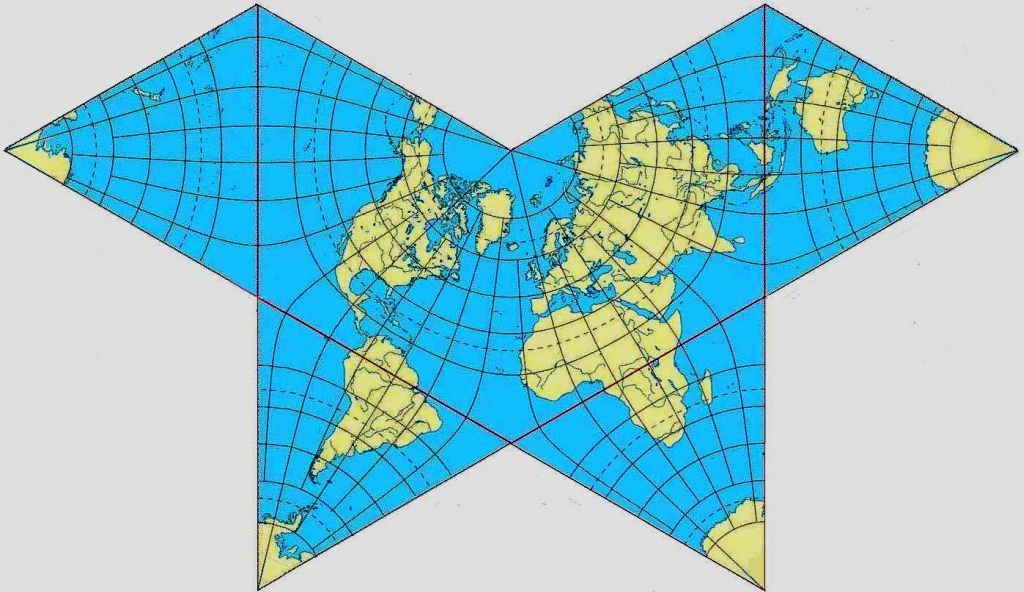
As I noted, one of my favorite map projections is Bartholomew's Regional Projection. But I must also have a soft spot for Cahill's Butterfly projection as well, given what I did with the Lambert conic conformal - I felt it was only fair to include an image here to show what I can achieve with it:

It might be possible to achieve a passable result using an Albers equal-area conic as well, with widely spaced standard parallels; 30 and 60 degrees on the projection seemed to work when I played with that in G.Projector.
Given that the above is the sort of map I favor, you can imagine what I think of the claim that the AuthaGraph map is perhaps the most accurate map ever made.

[daan]

Luca’s bat map plays on Cahill’s butterfly as well. I think it does a very good job.

I have love/hate feelings for replicating bits here and there to retain proximity.

— daan

[quadibloc]

Luca’s bat map plays on Cahill’s butterfly as well. I think it does a very good job.

I've begun coding a routine to draw the conformal version, with Dixon elliptic functions, of Cahill's butterfly. I got the polynomial to match Adams' tables (for his six-pointed star projection, from which I intend to convert). But there is still a lot of work ahead, and so I'm putting it off until I have the energy.

I still wanted to add a page to my site about the Dixon elliptic projections. I found one free program that handled them - written by Justin Kunimune, the man who reverse-engineered AuthaGraph. However, while it was able to draw the triangles for the butterfly for me, they were embedded in Luca's bat map. From which I had to carve them out to make the picture I wanted to put on my site.



So I have a love/hate relationship with Luca's bat map!

But you're right that replicating bits to maintain proximity - is an unfortunate solution. I did it there because... of how the projection constrained me in my options of interrupting it.

And I think interrupted projections are good, since distortion is bad. It would be nice if you could keep distortion "low enough" on an uninterrupted map of the whole world... but so many different solutions have been tried that it seems to me that it should be obvious there is no really satisfactory solution. Not that the Mercator, Winkel's Tripel, or the Briesemeister, or the Eckert IV are terrible, mind you, but trying to look for something that is much better than any of them and presents the entire world without any interruptions is likely a vain quest.

[daan]

I gave up on Dixon elliptic functions and instead reformulated all the Platonic solids faces in hypergeometric functions and wrote a general numerical solution to that. That turned out to be grotesquely painful… but marvelously general. No end of uses.

If you don’t have L.P. Lee’s 1976 monograph on conformal maps, I can heartily recommend it. While he dabbles in Dixon integrals and ultimately does not come up with a solution to the octahedral case, the book is chock full of other goodies. I was especially helped by his procedure for mapping a fixed fraction of the sphere to the half plane.

— daan

[quadibloc]

If you don’t have L.P. Lee’s 1976 monograph on conformal maps, I can heartily recommend it. While he dabbles in Dixon integrals and ultimately does not come up with a solution to the octahedral case, the book is chock full of other goodies. I was especially helped by his procedure for mapping a fixed fraction of the sphere to the half plane.

I don't have it, but the university I attended had a copy in their library, and I read and enjoyed it as a student. But the solution to the octahedral case is trivial - which is why Oscar S. Adams had no particular problem coming up with it for Cahill - basically, you just do the Lagrange projection stunt to some of the projections already in Oscar S. Adams' monograph on conformal projections from elliptic integrals. That's why Lee didn't bother to explain it.

[daan]

But the solution to the octahedral case is trivial - which is why Oscar S. Adams had no particular problem coming up with it for Cahill - basically, you just do the Lagrange projection stunt to some of the projections already in Oscar S. Adams' monograph on conformal projections from elliptic integrals. That's why Lee didn't bother to explain it.

What Lee has to say about that (p. 59):

Equation (39.3) is tantalizingly similar to (38.5), but a simple solution for r has not been obtained.

Thence Lee provides a series expansion, but notes,

This series is suitable for use when |R| ≯ 0.9. or within about 40° of the center of the trirectangular triangle, but is too slowly convergent beyond that distance.

With no further elaboration. Lee has no trouble giving explicit formulations for everything else in the book.

Adams does not address the octahedral case in Elliptic Functions Applied to Conformal World Maps (1925). I know Cahill credits Adams for his conformal butterfly’s mathematical development, but I don’t find any publication that obviously contains that. Adams published Conformal Projection of a Sphere Within a Square in 1929. That’s one I don’t have that, but the title doesn’t suggest it would be in there, and Snyder does not note a publication for Adams’s octahedral development, either.

So… I’m skeptical. But, perhaps you can enlighten us. I have a hypergeometric development, of course, and presumably that can be reformulated into elliptic integrals in some way, but that seems to have eluded Lee. He does give an illustration, but you only have to solve for specific points to get to that.

— daan